Show that $r=\frac{6}{2+\theta }$.

Find an expression for $V$ in terms of $\theta$.

Find the expression $\frac{dV}{d\theta }$.

Solve algebraically $\frac{dV}{d\theta }=0$ to find the value of $\theta$ that will maximize the volume, $V$.

$15=3+4r+2r\theta$                 M1

$12=2r\left(2+\theta \right)$                 A1

Note: Award A1 for any reasonable working leading to expected result e,g, factorizing $r$.

$r=\frac{6}{2+\theta }$                 AG

[2 marks]

attempt to use sector area to find volume                 (M1)

volume $=\frac{1}{2}{r}^2\theta \times 1$

$=\frac{1}{2}\times \frac{36}{{\left(2+\theta \right)}^2}\times \theta \left(=\frac{18\theta }{{\left(2+\theta \right)}^2}\right)$                 A1

[2 marks]

$\frac{dV}{d\theta }=\frac{{\left(2+\theta \right)}^2\times 18-36\theta \left(2+\theta \right)}{{\left(2+\theta \right)}^4}$              M1A1A1

$\frac{dV}{d\theta }=\frac{36-18\theta }{{\left(2+\theta \right)}^3}$

[3 marks]

$\frac{dV}{d\theta }=\frac{36-18\theta }{{\left(2+\theta \right)}^3}=0$             M1

Note: Award this M1 for simplified version equated to zero. The simplified version may have been seen in part (b)(ii).

$\theta =2$             A1

[2 marks]

Several candidates missed that the angle $\theta$ was in radians and used arc and sector formulas with degrees instead. This aside, part (a) was often well done. Part (b)(i) was also correctly answered by many candidates, but their failure to make any attempt to simplify their answer often led to difficulties in part (b)(ii). Again, failing to simplify the result in part (b)(ii) led to yet more difficulties in part (b)(iii). Some candidates used the product rule to differentiate $\frac{18\theta }{{\left(2+\theta \right)}^2}$ as $18\theta {\left(2+\theta \right)}^{-2}$ rather than the quotient rule. This was fine but made solving the equation in (b)(iii) less straightforward.

Several candidates missed that the angle $\theta$ was in radians and used arc and sector formulas with degrees instead. This aside, part (a) was often well done. Part (b)(i) was also correctly answered by many candidates, but their failure to make any attempt to simplify their answer often led to difficulties in part (b)(ii). Again, failing to simplify the result in part (b)(ii) led to yet more difficulties in part (b)(iii). Some candidates used the product rule to differentiate $\frac{18\theta }{{\left(2+\theta \right)}^2}$ as $18\theta {\left(2+\theta \right)}^{-2}$ rather than the quotient rule. This was fine but made solving the equation in (b)(iii) less straightforward.

Several candidates missed that the angle $\theta$ was in radians and used arc and sector formulas with degrees instead. This aside, part (a) was often well done. Part (b)(i) was also correctly answered by many candidates, but their failure to make any attempt to simplify their answer often led to difficulties in part (b)(ii). Again, failing to simplify the result in part (b)(ii) led to yet more difficulties in part (b)(iii). Some candidates used the product rule to differentiate $\frac{18\theta }{{\left(2+\theta \right)}^2}$ as $18\theta {\left(2+\theta \right)}^{-2}$ rather than the quotient rule. This was fine but made solving the equation in (b)(iii) less straightforward.

Several candidates missed that the angle $\theta$ was in radians and used arc and sector formulas with degrees instead. This aside, part (a) was often well done. Part (b)(i) was also correctly answered by many candidates, but their failure to make any attempt to simplify their answer often led to difficulties in part (b)(ii). Again, failing to simplify the result in part (b)(ii) led to yet more difficulties in part (b)(iii). Some candidates used the product rule to differentiate $\frac{18\theta }{{\left(2+\theta \right)}^2}$ as $18\theta {\left(2+\theta \right)}^{-2}$ rather than the quotient rule. This was fine but made solving the equation in (b)(iii) less straightforward.

Find the velocity vector of $P$.

Show that the acceleration vector of $P$ is never parallel to the position vector of $P$.

attempt at chain rule          (M1)

$\left(\mathit{v}=\frac{dOP}{dt}=\right) \left(\begin{array}{c}2t \cos t^2\\ -2t \sin t^2\end{array}\right)$          A1

[2 marks]

attempt at product rule         (M1)

$\mathit{a}=\left(\begin{array}{c}2 \cos t^2-4t^2 \sin t^2\\ -2 \sin t^2-4t^2 \cos t^2\end{array}\right)$          A1

METHOD 1

let $S=\sin t^2$ and  $C=\cos t^2$

finding $\cos \theta$ using

$\mathit{a}\mathbf{·}\overrightarrow{\text{OP}}=2SC-4t^2{S}^2-2SC-4t^2{C}^2=-4t^2$           M1

$\left|\overrightarrow{\text{OP}}\right|=1$

$\left|\mathit{a}\right|=\sqrt{{\left(2C-4t^{2}S\right)}^2+{\left(-2S-4t^{2}C\right)}^2}$

$=\sqrt{4+16t^4}>4t^2$

if $\theta$ is the angle between them, then

$\cos \theta =-\frac{4t^2}{\sqrt{4+16t^4}}$          A1

so $-1<\cos \theta <0$ therefore the vectors are never parallel          R1

METHOD 2

solve

$\left(\begin{array}{c}2 \cos t^2-4t^2 \sin t^2\\ -2 \sin t^2-4t^2 \cos t^2\end{array}\right)=k\left(\begin{array}{c}\sin t^2\\ \cos t^2\end{array}\right)$           M1

then

$\left(k=\right)\frac{2 \cos t^2-4t^2 \sin t^2}{\sin t^2}=\frac{-2 \sin t^2-4t^2 \cos t^2}{\cos t^2}$

Note: Condone candidates not excluding the division by zero case here. Some might go straight to the next line.

$2 {\cos }^2 t^2-4t^2\cos t^2 \sin t^2=-2 {\sin }^2 t^2-4t^2 \cos t^2 \sin t^2$

$2 {\cos }^2 t^2+2 {\sin }^2 t^2=0$

$2=0$          A1

this is never true so the two vectors are never parallel          R1

METHOD 3

embedding vectors in a 3d space and taking the cross product:            M1

$\left(\begin{array}{c}\sin t^2\\ \cos t^2\\ 0\end{array}\right)\times \left(\begin{array}{c}2 \cos t^2-4t^2 \sin t^2\\ -2 \sin t^2-4t^2 \cos t^2 \\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ -2 {\sin }^2 t^2-4t^2 \cos t^2 \sin t^2-2 {\cos }^2 t^2+4t^2 \cos t^2 \sin t^2 \end{array}\right)$

                     $=\left(\begin{array}{c}0\\ 0\\ -2\end{array}\right)$          A1

since the cross product is never zero, the two vectors are never parallel          R1

[5 marks]

In part (a), many candidates found the velocity vector correctly. In part (b), however, many candidates failed to use the product rule correctly to find the acceleration vector. To show that the acceleration vector is never parallel to the position vector, a few candidates put $\stackrel{\mathbf{.}\mathbf{.}}{\mathit{r}}=k\mathit{r}$ presumably hoping to show that no value of the constant k existed for any t but this usually went nowhere.

Write down the value of $a$.

Find the value of $b$.

The outer dome of a large cathedral has the shape of a hemisphere of diameter 32 m, supported by vertical walls of height 17 m. It is also supported by an inner dome which can be modelled by rotating the curve $y=33-0.08x^3$ through 360° about the $y$-axis between $y$ = 0 and $y$ = 33, as indicated in the diagram.

Find the volume of the space between the two domes.

$a$ = 33    A1

[1 mark]

$\frac{1}{\sqrt[3]{0.08}}=2.32$     M1A1

[2 marks]

volume within outer dome

$\frac{2}{3}\pi +{16}^3+\pi \times {16}^2\times 17=22250.85$      M1A1

volume within inner dome

$\pi {\int }_0^{33}{\left(\frac{33-y}{0.08}\right)}^{\frac{2}{3}}\text{d}y=3446.92$       M1A1

volume between = 22 250.85 − 3446.92 = 18 803.93 m³       A1

[5 marks]

A function $f$ is of the form $f\left(t\right)=p{\text{e}}^{q \cos \left(rt\right)}, p, q, r\in {\mathrm{ℝ}}^{+}$. Part of the graph of $f$ is shown.

The points $\text{A}$ and $\text{B}$ have coordinates $\text{A}(0, 6.5)$ and $\text{B}(5.2, 0.2)$, and lie on $f$.

The point $\text{A}$ is a local maximum and the point $\text{B}$ is a local minimum.

Find the value of $p$, of $q$ and of $r$.

substitute coordinates of $\text{A}$

$f\left(0\right)=p{\text{e}}^{q \cos \left(0\right)}=6.5$

$6.5=p{\text{e}}^q$             (A1)

substitute coordinates of $\text{B}$

$f\left(5.2\right)=p{\text{e}}^{q \cos \left(5.2r\right)}=0.2$

EITHER

$f\text{'}\left(t\right)=-pqr \sin \left(rt\right){\text{e}}^{q \cos \left(rt\right)}$             (M1)

minimum occurs when $-pqr \sin \left(5.2r\right){\text{e}}^{q \cos \left(5.2r\right)}=0$

$\sin \left(rt\right)=0$

$r\times 5.2=\mathrm{\pi }$             (A1)

OR

minimum value occurs when $\cos \left(rt\right)=-1$             (M1)

$r\times 5.2=\mathrm{\pi }$             (A1)

OR

period $=2\times 5.2=10.4$             (A1)

$r=\frac{2\mathrm{\pi }}{10.4}$             (M1)

THEN

$r=\frac{\mathrm{\pi }}{5.2}=0.604152\dots \left(0.604\right)$             A1

$0.2=p {\text{e}}^{-q}$             (A1)

eliminate $p$ or $q$             (M1)

${\text{e}}^{2q}=\frac{6.5}{0.2}$   OR   $0.2=\frac{p^2}{6.5}$

$q=1.74 \left(1.74062\dots \right)$             A1

$p=1.14017\dots \left(1.14\right)$             A1

[8 marks]

This was a challenging question and suitably positioned at the end of the examination. Candidates who attempted it were normally able to substitute points A and B into the given equation. Some were able to determine the first derivative. Only a few candidates were able to earn significant marks for this question.

Find ${\int }_0^5\frac{1000}{2+t}\text{d}t$.

State in context what this value represents.

Find an expression for $P$ in terms of $t$.

Determine ${\int }_0^{365}P\left(t\right) \text{d}t$ and state what it represents.

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

$1252.7\dots \approx 1250$ (barrels per day)        A1

[1 mark]

This is the increase (change) in $P$ (production per day) between $t=0$ and $t=5$ (or during the first $5$ days)       A1

[1 mark]

METHOD 1

$P=1000 \ln \left(2+t\right)+c$        (M1)A1

$c=20000-1000 \ln 2\approx 19306.8\dots$        (M1)A1

$P=1000 \ln \left(2+t\right)+19300$

METHOD 2

$\underset{20000}{\overset{P}{\int }}\text{d}P=\underset{0}{\overset{t}{\int }}\frac{1000}{2+x}\text{d}x$        (M1)

${\left[P\right]}_{20000}^P=1000{\left[\ln \left(2+x\right)\right]}_0^t$        A1

Note: A1 is for the correct integral, with the correct limits.

$P-20000=1000\left(\ln \left(2+t\right)-\ln 2\right)$        (M1)A1

$P=1000 \ln \left(\frac{2+t}{2}\right)+20000$

[4 marks]

$8847883\approx 8850000$ (barrels)        A1

Total production of oil in barrels in the first year (or first $365$ days)        A1

Note: For the final A1 “barrels”’ must be present either in the statement or as the units.

Accept any value which rounds correctly to $8850000$

[2 marks]

Show that $V={\left(20-\frac{t}{5}\right)}^2$.

Find the time taken for the tank to empty.

$\frac{dV}{dt}=-k{V}^{\frac{1}{2}}$

use of separation of variables               (M1) 

$\Rightarrow \int V^{-\frac{1}{2}} \text{d}V=\int -k \text{d}t$               A1 

$2V^{\frac{1}{2}}=-kt \left(+c\right)$               A1 

considering initial conditions $40=c$               A1 

$2\sqrt{324}=-10k+40$

$\Rightarrow k=0.4$               A1 

$2\sqrt{V}=-0.4t+40$

$\Rightarrow \sqrt{V}=20-0.2t$               A1 

Note: Award A1 for any correct intermediate step that leads to the AG.

$\Rightarrow V={\left(20-\frac{t}{5}\right)}^2$                  AG

Note: Do not award the final A1 if the AG line is not stated.

[6 marks]

$0={\left(20-\frac{t}{5}\right)}^2\Rightarrow t=100$ minutes               (M1)A1

[2 marks]

Find $f\text{'}\left(x\right)$.

Find in terms of $a$ the value of $x$ at which the maximum occurs.

Hence find the value of $a$ for which $y$ has the smallest possible maximum value.

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

$f\text{'}\left(x\right)=\left(-2ax+1\right)\times \frac{1}{2}\times {\left(-a{x}^2+x+a\right)}^{-\frac{1}{2}}$

Note: M1 is for use of the chain rule.

$=\frac{-2ax+1}{2\sqrt{-a{x}^2+x+a}}$         M1A1

[2 marks]

$-2ax+1=0$         (M1)

$x=\frac{1}{2a}$       A1

[2 marks]

Value of local maximum $=\sqrt{-a\times \frac{1}{4a^2}+\frac{1}{2a}+a}$         M1A1

$=\sqrt{\frac{1}{4a}+a}$

This has a minimum value when $a=0.5$         (M1)A1

[4 marks]

The graph of $y=f\left(x\right)$ has a local maximum at A. Find the coordinates of A.

Show that there is exactly one point of inflexion, B, on the graph of $y=f\left(x\right)$.

The coordinates of B can be expressed in the form B$\left(2^a,b\times 2^{-3a}\right)$ where a, b$\in \mathbb{Q}$. Find the value of a and the value of b.

Sketch the graph of $y=f\left(x\right)$ showing clearly the position of the points A and B.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to differentiate      (M1)

$f^{\prime }\left(x\right)=-3x^{-4}-3x$     A1

Note: Award M1 for using quotient or product rule award A1 if correct derivative seen even in unsimplified form, for example $f^{\prime }\left(x\right)=\frac{-15x^4\times 2x^3-6x^2\left(2-3x^5\right)}{{\left(2x^3\right)}^2}$.

$-\frac{3}{x^4}-3x=0$     M1

$\Rightarrow x^5=-1\Rightarrow x=-1$     A1

$\text{A}\left(-1,-\frac{5}{2}\right)$     A1

[5 marks]

$f^{″}\left(x\right)=0$     M1

$f^{″}\left(x\right)=12x^{-5}-3\left(=0\right)$     A1

Note: Award A1 for correct derivative seen even if not simplified.

$\Rightarrow x=\sqrt[5]{4}\left(=2^{\frac{2}{5}}\right)$     A1

hence (at most) one point of inflexion      R1

Note: This mark is independent of the two A1 marks above. If they have shown or stated their equation has only one solution this mark can be awarded.

$f^{″}\left(x\right)$ changes sign at $x=\sqrt[5]{4}\left(=2^{\frac{2}{5}}\right)$      R1

so exactly one point of inflexion

[5 marks]

$x=\sqrt[5]{4}=2^{\frac{2}{5}}\left(\Rightarrow a=\frac{2}{5}\right)$      A1

$f\left(2^{\frac{2}{5}}\right)=\frac{2-3\times 2^2}{2\times 2^{\frac{6}{5}}}=-5\times 2^{-\frac{6}{5}}\left(\Rightarrow b=-5\right)$     (M1)A1

Note: Award M1 for the substitution of their value for $x$ into $f\left(x\right)$.

[3 marks]

A1A1A1A1

A1 for shape for x < 0
A1 for shape for x > 0
A1 for maximum at A
A1 for POI at B.

Note: Only award last two A1s if A and B are placed in the correct quadrants, allowing for follow through.

[4 marks]

Identify the $x$ value of the point where $|h\prime (x\left)\right|$ has its maximum value.

Interpret this point in the given context.

Juri starts at a height of $60$ metres and finishes at $\text{F}$, where $x=f$.

Sketch a possible diagram of the hill on the following pair of coordinate axes.

$a$             A1

[1 mark]

the hill is at its steepest / largest slope of hill              A1

[1 mark]

            A1A1A1

Note: Award (A1) for decreasing function from $0$ to $b$ and $d$ to $f$ and increasing from $b$ to $d$; (A1) for minimum at $b$ and max at $d$; (A1) for starting at height of $60$ and finishing at a height of $0$ at $f$. If reasonable curvature not evident on graph (i.e. only straight lines used) award A1A0A1.

[3 marks]

This was one of the weakest questions on the paper. Many candidates failed to appreciate the significance of the absolute value and gave $c$ as the maximum value rather than $a$. Another common error was to interpret the maximum value as greatest velocity or highest point rather than the point where the hill was steepest. A few candidates drew a graph that went from the starting point to the finishing point. What happened in between, often, showed little understanding of the relationship between the graphs of a function and its derivative. The section of the syllabus that mentions understanding derivatives through graphical methods needs more support from teachers.

This was one of the weakest questions on the paper. Many candidates failed to appreciate the significance of the absolute value and gave $c$ as the maximum value rather than $a$. Another common error was to interpret the maximum value as greatest velocity or highest point rather than the point where the hill was steepest. A few candidates drew a graph that went from the starting point to the finishing point. What happened in between, often, showed little understanding of the relationship between the graphs of a function and its derivative. The section of the syllabus that mentions understanding derivatives through graphical methods needs more support from teachers.

Calculate the value of $\frac{dy}{dx}$ at the point $(0, 1)$.

Sketch, on the first graph, a curve that represents the points where $\frac{dy}{dx}=0$.

(i)   sketch the solution curve that passes through the point $(0, 0)$.

(ii)  sketch the solution curve that passes through the point $(0, 0.75)$.

$\left(\frac{dy}{dx}={\text{e}}^0-1\right)=0$                 A1

[1 mark]

gradient $=0$ at $\left(0, 1\right)$                 A1

correct shape                 A1

 
Note: Award second A1 for horizontal asymptote of $y=0$, and general symmetry about the $y$-axis.

[2 marks]

(i)  positive gradient at origin              A1

      correct shape                 A1

 
Note: Award second A1 for a single maximum in 1^st quadrant and tending toward an asymptote.

(ii)  positive gradient at $(0, 0.75)$                 A1

      correct shape                 A1

Note: Award second A1 for a single minimum in 2^nd quadrant, single maximum in 1^st quadrant and tending toward an asymptote.

[4 marks]

There were many good attempts at this question. Care needs to be taken over graph sketching, and the existence of asymptotes or the position of intersections needs to be shown clearly. Many candidates correctly found $\frac{\mathrm{d}y}{\mathrm{d}x}=0$ at $\left(0,1\right)$ in part (a). However, they were then misled into finding a solution curve through this point rather than graphing the points where $\frac{\mathrm{d}y}{\mathrm{d}x}=0$ as required in part (b). Part (c) was answered well with a number of correct answers. Often the curve through $\left(0,0.75\right)$ had a flat central section and did not show a clear maximum and minimum. The asymptotes were generally poorly drawn with the curves meeting the $x$-axis and stopping or worse still crossing over it.

There were many good attempts at this question. Care needs to be taken over graph sketching, and the existence of asymptotes or the position of intersections needs to be shown clearly. Many candidates correctly found $\frac{\mathrm{d}y}{\mathrm{d}x}=0$ at $\left(0,1\right)$ in part (a). However, they were then misled into finding a solution curve through this point rather than graphing the points where $\frac{\mathrm{d}y}{\mathrm{d}x}=0$ as required in part (b). Part (c) was answered well with a number of correct answers. Often the curve through $\left(0,0.75\right)$ had a flat central section and did not show a clear maximum and minimum. The asymptotes were generally poorly drawn with the curves meeting the $x$-axis and stopping or worse still crossing over it.

There were many good attempts at this question. Care needs to be taken over graph sketching, and the existence of asymptotes or the position of intersections needs to be shown clearly. Many candidates correctly found $\frac{\mathrm{d}y}{\mathrm{d}x}=0$ at $\left(0,1\right)$ in part (a). However, they were then misled into finding a solution curve through this point rather than graphing the points where $\frac{\mathrm{d}y}{\mathrm{d}x}=0$ as required in part (b). Part (c) was answered well with a number of correct answers. Often the curve through $\left(0,0.75\right)$ had a flat central section and did not show a clear maximum and minimum. The asymptotes were generally poorly drawn with the curves meeting the $x$-axis and stopping or worse still crossing over it.

Expand ${\left(\frac{1}{u}+1\right)}^2$.

Find $\int {\left(\frac{1}{\left(x+2\right)}+1\right)}^{2}dx$.

Find the volume of the solid formed. Give your answer in the form $\frac{\mathrm{\pi }}{4}\left(a+b \ln \left(c\right)\right)$, where $a, b, c\in \mathrm{\mathbb{Z}}$.

$\frac{1}{u^2}+\frac{2}{u}+1$             A1

[1 mark]

$\int {\left(\frac{1}{\left(x+2\right)}+1\right)}^{2}dx$

$=\int \left(\frac{1}{{\left(x+2\right)}^2}+\frac{2}{x+2}+1\right)dx$   OR   $\int \left(\frac{1}{u^2}+\frac{2}{u}+1\right)du$             (M1)

$=-\frac{1}{\left(x+2\right)}+2 \ln \left|x+2\right|+x\left(+c\right)$             A1A1

Note: Award A1 for first expression, A1 for second two expressions.
Award A1A0 for a final answer of $=-\frac{1}{u}+2 \ln \left(u\right)+u\left(+c\right)$.

[3 marks]

volume $=\mathrm{\pi }{\left[-\frac{1}{\left(x+2\right)}+2 \ln \left(x+2\right)+x\right]}_0^2$             M1

$=\mathrm{\pi }\left(-\frac{1}{4}+2 \ln \left(4\right)+2+\frac{1}{2}-2 \ln 2\right)$             A1

$=\mathrm{\pi }\left(\frac{9}{4}+2 \ln \left(4\right)-2 \ln 2\right)$

use of log laws seen, for example             M1

$\mathrm{\pi }\left(\frac{9}{4}+4 \ln \left(2\right)-2 \ln 2\right)$   OR   $\mathrm{\pi }\left(\frac{9}{4}+2 \ln \left(\frac{4}{2}\right)\right)$

$=\frac{\mathrm{\pi }}{4}\left(9+8 \ln \left(2\right)\right)$   OR   $a=9, b=8$ and $c=2$             A1

Note: Other correct integer solutions are possible and should be accepted for example $a=9, b=c=4$.

[4 marks]

Some candidates could answer part (a) (i). The link between parts (i) and (ii) was, however, lost to the majority. Those who did see the link were often able to give a reasonable answer to (ii). But some candidates lacked the skills to integrate without the use of technology, so an indefinite integral presented many problems. Even those who successfully navigated part (a) went on to fail to see the link to part (b). Either the integration was attempted as something totally new and unconnected or it was simply found with the GDC which did not lead to a final answer in the required form.

Find $\frac{dy}{dx}$.

Find $\frac{{\text{d}}^{2}y}{d{x}^2}$.

The curve has a point of inflexion at $\left(a, b\right)$.

Find the value of $a$.

use of product rule         (M1)

$\frac{dy}{dx}=2\left(4-{\text{e}}^x\right)+2x\left(-{\text{e}}^x\right)$         A1

$=8-2{\text{e}}^x-2x{\text{e}}^x$

[2 marks]

use of product rule         (M1)

$\frac{d^{2}y}{d{x}^2}=-2{\text{e}}^x-2{\text{e}}^x-2x{\text{e}}^x$         A1

$=-4{\text{e}}^x-2x{\text{e}}^x$

$=-2\left(2+x\right){\text{e}}^x$

[2 marks]

$-2\left(2+a\right){\text{e}}^a=0$  OR  sketch of $\frac{d^{2}y}{d{x}^2}$ with $x$-intercept indicated  OR  finding the local maximum of $\frac{dy}{dx}$ at $\left(-2, 8.27\right)$         (M1)

$\left(a=\right) -2$         A1

[2 marks]

Some candidates attempted to apply the product rule in parts (a)(i) and (ii) but often incorrectly, particularly in part (ii) when finding $\frac{{\text{d}}^{2}y}{\text{d}{x}^2}$. In part (b) there was little understanding shown of the point of inflexion. There were some attempts, some of which were correct, but many where either the function or the first derivative were set to zero rather than the second derivative.

Find the value of $\frac{\text{d}y}{\text{d}x}$ when $t=0$.

On the following axes, sketch a possible trajectory for the growth of the two fungi, making clear any asymptotic behaviour.

$\frac{\text{d}y}{\text{d}x}=\frac{16-20}{24-20}$     M1

= −1     A1

[2 marks]

asymptote of trajectory along r $=k\left(\begin{array}{c}2\\ 1\end{array}\right)$   M1A1

Note: Award M1A0 if asymptote along $\left(\begin{array}{c}1\\ 2\end{array}\right)$.

trajectory begins at (8, 10) with negative gradient    A1A1

[4 marks]

Express $x^2+3x+2$ in the form $(x+h{)}^2+k$.

Factorize $x^2+3x+2$.

Sketch the graph of $f(x)$, indicating on it the equations of the asymptotes, the coordinates of the $y$-intercept and the local maximum.

Show that $\frac{1}{x+1}-\frac{1}{x+2}=\frac{1}{x^2+3x+2}$.

Hence find the value of $p$ if ${\int }_0^{1}f(x)\text{d}x=\ln (p)$.

Sketch the graph of $y=f\left(\left|x\right|\right)$.

Determine the area of the region enclosed between the graph of $y=f\left(\left|x\right|\right)$, the $x$-axis and the lines with equations $x=-1$ and $x=1$.

$x^2+3x+2={\left(x+\frac{3}{2}\right)}^2-\frac{1}{4}$     A1

[1 mark]

$x^2+3x+2=(x+2)(x+1)$     A1

[1 mark]

A1 for the shape

A1 for the equation $y=0$

A1 for asymptotes $x=-2$ and $x=-1$

A1 for coordinates $\left(-\frac{3}{2},-4\right)$

A1 $y$-intercept $\left(0,\frac{1}{2}\right)$

[5 marks]

$\frac{1}{x+1}-\frac{1}{x+2}=\frac{(x+2)-(x+1)}{(x+1)(x+2)}$     M1

$=\frac{1}{x^2+3x+2}$     AG

[1 mark]

$\underset{0}{\overset{1}{\int }}\frac{1}{x+1}-\frac{1}{x+2}\text{d}x$

$={\left[\ln (x+1)-\ln (x+2)\right]}_0^1$     A1

$=\ln 2-\ln 3-\ln 1+\ln 2$     M1

$=\ln \left(\frac{4}{3}\right)$     M1A1

$\therefore p=\frac{4}{3}$

[4 marks]

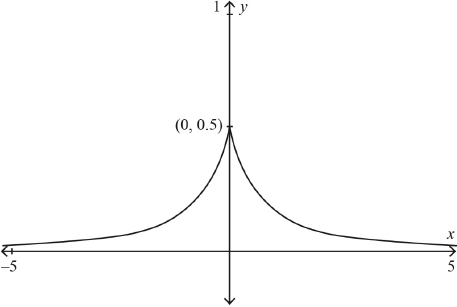
symmetry about the $y$-axis     M1

correct shape     A1

Note:     Allow FT from part (b).

[2 marks]

$2{\int }_0^{1}f(x)\text{d}x$     (M1)(A1)

$=2\ln \left(\frac{4}{3}\right)$     A1

Note:     Do not award FT from part (e).

[3 marks]

Write down an expression for $E$ as a function of time.

Hence find $\frac{\text{d}E}{\text{d}t}$.

Hence or otherwise find the first time at which the kinetic energy is changing at a rate of 5 J s⁻¹.

$E=5{\left(2\text{sin}t\right)}^2\left(=20\text{si}{\text{n}}^{2}t\right)$     A1

[1 mark]

$\frac{\text{d}E}{\text{d}t}=40\text{sin}t\text{cos}t$    (M1)A1

[2 marks]

$t$ = 0.126   (M1)A1

[2 marks]

Write down the $x$-coordinate of the point of inflexion on the graph of $y=f\left(x\right)$.

find the value of $f\left(1\right)$.

find the value of $f\left(4\right)$.

Sketch the curve $y=f\left(x\right)$, 0 ≤ $x$ ≤ 5 indicating clearly the coordinates of the maximum and minimum points and any intercepts with the coordinate axes.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

3     A1

[1 mark]

attempt to use definite integral of $f^{\prime }\left(x\right)$        (M1)

${\int }_0^1{f}^{\prime }\left(x\right)\text{d}x=0.5$

$f\left(1\right)-f\left(0\right)=0.5$        (A1)

$f\left(1\right)=0.5+3$

= 3.5      A1

[3 marks]

${\int }_1^4{f}^{\prime }\left(x\right)\text{d}x=-2.5$       (A1)

Note: (A1) is for −2.5.

$f\left(4\right)-f\left(1\right)=-2.5$

$f\left(4\right)=3.5-2.5$

= 1      A1

[2 marks]

    A1A1A1

A1 for correct shape over approximately the correct domain
A1 for maximum and minimum (coordinates or horizontal lines from 3.5 and 1 are required),
A1 for $y$-intercept at 3

[3 marks]

Show that $\text{lo}{\text{g}}_{r^2}x=\frac{1}{2}\text{lo}{\text{g}}_{r}x$ where $r,x\in {\mathbb{R}}^{+}$.

Express $y$ in terms of $x$. Give your answer in the form $y=p{x}^q$, where p , q are constants.

The region R, is bounded by the graph of the function found in part (b), the x-axis, and the lines $x=1$ and $x=\alpha$ where $\alpha >1$. The area of R is $\sqrt{2}$.

Find the value of $\alpha$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1

$\text{lo}{\text{g}}_{r^2}x=\frac{\text{lo}{\text{g}}_{r}x}{\text{lo}{\text{g}}_r{r}^2}\left(=\frac{\text{lo}{\text{g}}_{r}x}{\text{2}\text{lo}{\text{g}}_{r}r}\right)$     M1A1

$=\frac{\text{lo}{\text{g}}_{r}x}{2}$     AG

[2 marks]

METHOD 2

$\text{lo}{\text{g}}_{r^2}x=\frac{1}{\text{lo}{\text{g}}_x{r}^2}$     M1

$=\frac{1}{2\text{lo}{\text{g}}_{x}r}$     A1

$=\frac{\text{lo}{\text{g}}_{r}x}{2}$     AG

[2 marks]

METHOD 1

$\text{lo}{\text{g}}_{2}y+\text{lo}{\text{g}}_{4}x+\text{lo}{\text{g}}_{4}2x=0$

$\text{lo}{\text{g}}_{2}y+\text{lo}{\text{g}}_{4}2x^2=0$     M1

$\text{lo}{\text{g}}_{2}y+\frac{1}{2}\text{lo}{\text{g}}_{2}2x^2=0$     M1

$\text{lo}{\text{g}}_{2}y=-\frac{1}{2}\text{lo}{\text{g}}_{2}2x^2$

$\text{lo}{\text{g}}_{2}y=\text{lo}{\text{g}}_2\left(\frac{1}{\sqrt{2x}}\right)$     M1A1

$y=\frac{1}{\sqrt{2}}{x}^{-1}$     A1

Note: For the final A mark, $y$ must be expressed in the form $p{x}^q$.

[5 marks]

METHOD 2

$\text{lo}{\text{g}}_{2}y+\text{lo}{\text{g}}_{4}x+\text{lo}{\text{g}}_{4}2x=0$

$\text{lo}{\text{g}}_{2}y+\frac{1}{2}\text{lo}{\text{g}}_{2}x+\frac{1}{2}\text{lo}{\text{g}}_{2}2x=0$     M1

$\text{lo}{\text{g}}_{2}y+\text{lo}{\text{g}}_2{x}^{\frac{1}{2}}+\text{lo}{\text{g}}_2{\left(2x\right)}^{\frac{1}{2}}=0$     M1

$\text{lo}{\text{g}}_2\left(\sqrt{2}xy\right)=0$     M1

$\sqrt{2}xy=1$     A1

$y=\frac{1}{\sqrt{2}}{x}^{-1}$     A1

Note: For the final A mark, $y$ must be expressed in the form $p{x}^q$.

[5 marks]

the area of R is $\underset{1}{\overset{\alpha }{\int }}\frac{1}{\sqrt{2}}{x}^{-1}\text{d}x$     M1

$={\left[\frac{1}{\sqrt{2}}\text{ln}x\right]}_1^{\alpha }$     A1

$=\frac{1}{\sqrt{2}}\text{ln}\alpha$     A1

$\frac{1}{\sqrt{2}}\text{ln}\alpha =\sqrt{2}$     M1

$\alpha ={\text{e}}^2$     A1

Note: Only follow through from part (b) if $y$ is in the form $y=p{x}^q$

[5 marks]

Write the differential equation as a system of coupled first order differential equations.

When $t=0$, $x=\dot{x}=0$

Use Euler’s method with a step length of $0.1$ to find an estimate for the value of the displacement and velocity of the particle when $t=1$.

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

$\dot{x}=y$        M1

$\dot{y}=2t-4y^2$         A1

[2 marks]

$t_{n+1}=t_n+0.1$

$x_{n+1}=x_n+0.1y_n$

$y_{n+1}=y_n+0.1\left(2t_n-4y_n^2\right)$         (M1)(A1)

Note: Award M1 for a correct attempt to substitute the functions in part (a) into the formula for Euler’s method for coupled systems.

When $t=1$

$x=0.202 \left(0.20201\dots \right)$         A1

$\dot{x}=0.598 \left(0.59822\dots \right)$         A1

Note: Accept $y=0.598$.

[4 marks]

Find an expression for $\frac{dW}{dv}$.

When Frieda arrives at the top of a hill, the speed of the wind is $10$ kilometres per hour and increasing at a rate of $5 {\text{km\hspace{0.05em}h}}^{-1} {\text{minute}}^{-1}$.

Find the rate of change of $W$ at this time.

use of power rule             (M1)

$\frac{dW}{dv}=-1.1848v^{-0.84}$   OR   $-1.18v^{-0.84}$            A1

[2 marks]

$\frac{dv}{dt}=5$             (A1)

$\frac{dW}{dt}=\frac{dv}{dt}\times \frac{dW}{dv}$             (M1)

$\left(\frac{dW}{dt}=-5\times 1.1848v^{-0.84}\right)$

when $v=10$

$\frac{dW}{dt}=-5\times 1.1848\times {10}^{-0.84}$             (M1)

$-0.856 \left(-0.856278\dots \right) °{\text{C\hspace{0.05em}min}}^{-1}$             A2

Note: Accept a negative answer communicated in words, “decreasing at a rate of…”.
Accept a final answer of $-0.852809\dots °{\text{C\hspace{0.05em}min}}^{-1}$ from use of $-1.18$.
Accept $51.4$ (or $51.2$)$°{\text{C\hspace{0.05em}hour}}^{-1}$.

[5 marks]

There was some success in using the power rule to differentiate the function in part (a). Many failed to recognize that part (b) was a related rates of change problem. There was also confusion about the term “rate of change” and with the units used in this question.

Write down the equation of the curve on which all these maximum and minimum points lie.

Sketch this curve on the slope field.

The solution to the differential equation that passes through the point $(0, -2)$ has both a local maximum point and a local minimum point.

On the slope field, sketch the solution to the differential equation that passes through $(0, -2)$.

$x^2+\frac{y}{2}=0 \left(y=-2x^2\right)$           A1

[1 mark]

$y=-2x^2$ drawn on diagram (correct shape with a maximum at $(0,0)$)        A1

[1 mark]

correct shape with a local maximum and minimum, passing through $(0, -2)$         A1

local maximum and minimum on the graph of $y=-2x^2$         A1

[2 marks]

This question was very poorly done and frequently left blank. Few candidates understood the connection between the differential equation and maximum and minimum points. Even when the equation $\frac{\text{d}y}{\text{d}x}=0$ was correctly solved, it was rare to see the curve correctly drawn on the slope field. Some were able to draw a solution to the differential equation on the slope field though often not through the given initial condition.

Show that the volume of water, $V$, in terms of $h$ is $V=3\mathrm{\pi }\left({\mathrm{e}}^{\frac{h}{3}}-1\right)$.

Hence find the maximum capacity of the bowl in ${\text{cm}}^3$.

attempt to use $V=\mathrm{\pi }{\int }_a^b{x}^2 dy$             (M1)

$x={\text{e}}^{\frac{y}{6}}$ or any reasonable attempt to find $x$ in terms of $y$             (M1)

$V=\mathrm{\pi }{\int }_0^h{\text{e}}^{\frac{y}{3}} dy$             A1

Note: Correct limits must be seen for the A1 to be awarded.

$=\mathrm{\pi }{\left[3{\text{e}}^{\frac{y}{3}}\right]}_0^h$             (A1)

Note: Condone the absence of limits for this A1 mark.

$=3\mathrm{\pi }\left[{\text{e}}^{\frac{h}{3}}-{\text{e}}^0\right]$             A1

$=3\mathrm{\pi }\left[{\text{e}}^{\frac{h}{3}}-1\right]$             AG

Note: If the variable used in the integral is $x$ instead of $y$ (i.e. $V=\mathrm{\pi }{\int }_0^h{\text{e}}^{\frac{x}{3}} dx$) and the candidate has not stated that they are interchanging $x$ and $y$ then award at most M1M1A0A1A1AG.

[5 marks]

maximum volume when $h=9 \text{cm}$             (M1)

max volume $=180 {\text{cm}}^3$             A1

[2 marks]

A number of candidates switched variables so that $y=6\ln x$ and then used $\mathrm{\pi }\int y^2\mathrm{d}x$. Other candidates who correctly found $x$ in terms of $y$ failed to use the limits $0$ and $h$, using $0$ and $9$ instead. As part (a) was to show that the volume was equal to the final expression it was necessary for examiners to see steps in obtaining the result. It was common to miss out any expression involving ${\mathrm{e}}^0$. Since the value $1$ could be written from the answer given, where this value came from needed to be shown. It was encouraging to see correct answers to (b), even when candidates had failed to gain marks for (a). Some candidates successfully used their GDC to calculate the value of the definite integral numerically.

A number of candidates switched variables so that $y=6\ln x$ and then used $\mathrm{\pi }\int y^2\mathrm{d}x$. Other candidates who correctly found $x$ in terms of $y$ failed to use the limits $0$ and $h$, using $0$ and $9$ instead. As part (a) was to show that the volume was equal to the final expression it was necessary for examiners to see steps in obtaining the result. It was common to miss out any expression involving ${\mathrm{e}}^0$. Since the value $1$ could be written from the answer given, where this value came from needed to be shown. It was encouraging to see correct answers to (b), even when candidates had failed to gain marks for (a). Some candidates successfully used their GDC to calculate the value of the definite integral numerically.

The shape of a vase is formed by rotating a curve about the $y$-axis.

The vase is $10 \text{cm}$ high. The internal radius of the vase is measured at $2 \text{cm}$ intervals along the height:

Use the trapezoidal rule to estimate the volume of water that the vase can hold.

$V=\mathrm{\pi }\underset{0}{\overset{10}{\int }}{y}^2 dx$   OR   $\mathrm{\pi }\underset{0}{\overset{10}{\int }}{x}^2 dy$          (M1)

$h=2$

$\approx \mathrm{\pi }\times \frac{1}{2}\times 2\times \left(\left(4^2+5^2\right)+2\times \left(6^2+8^2+7^2+3^2\right)\right)$        M1A1

$=1120 {\text{cm}}^3 \left(1121.548\dots \right)$          A1

Note: Do not award the second M1 If the terms are not squared.

[4 marks]

This was a straightforward question on the trapezoidal rule, presented in an unfamiliar way, but only a tiny minority answered it correctly. It may be that candidates were introduced to the trapezium rule as an approximation to the area under a curve and here they were being asked to find an approximation to a volume and they were unable to see how that could be done.

Find $\frac{\text{d}y}{\text{d}\theta }$

Hence find the values of θ for which $\frac{\text{d}y}{\text{d}\theta }=2y$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt at chain rule or product rule     (M1)

$\frac{\text{d}y}{\text{d}\theta }=2\text{sin}\theta \text{cos}\theta$     A1

[2 marks]

$2\text{sin}\theta \text{cos}\theta =2\text{si}{\text{n}}^2\theta$

sin θ = 0     (A1)

θ = 0, $\pi$     A1

obtaining cos θ = sin θ     (M1)

tan θ = 1     (M1)

$\theta =\frac{\pi }{4}$     A1

[5 marks]

Find the area of the window in terms of P and $r$.

Find the width of the window in terms of P when the area is a maximum, justifying that this is a maximum.

Show that in this case the height of the rectangle is equal to the radius of the semicircle.

the width of the rectangle is $2r$ and let the height of the rectangle be $h$

$P=2r+2h+\pi r$     (A1)

$A=2rh+\frac{\pi r^2}{2}$     (A1)

$h=\frac{\text{P}-2r-\pi r}{2}$

$A=2r\left(\frac{\text{P}-2r-\pi r}{2}\right)+\frac{\pi r^2}{2}\left(=\mathrm{P}r-2r^2-\frac{\pi r^2}{2}\right)$     M1A1

[4 marks]

$\frac{\text{d}A}{\text{d}r}=\text{P}-4r-\pi r$     A1

$\frac{\text{d}A}{\text{d}r}=0$     M1

$\Rightarrow r=\frac{\text{P}}{4+\pi }$     (A1)

hence the width is $\frac{2\text{P}}{4+\pi }$     A1

     R1

hence maximum     AG

[5 marks]

EITHER

$h=\frac{\text{P}-2r-\pi r}{2}$

$h=\frac{\text{P}-\frac{2\text{P}}{4+\pi }-\frac{\text{P}\pi }{4+\pi }}{2}$     M1

$h=\frac{4\text{P}+\pi \text{P}-2\text{P}-\pi \text{P}}{2(4+\pi )}$    A1

$h=\frac{\text{P}}{(4+\pi )}=r$     AG

OR

$h=\frac{\text{P}-2r-\pi r}{2}$

$P=r(4+\pi )$     M1

$h=\frac{r(4+\pi )-2r-\pi r}{2}$     A1

$h=\frac{4r+\pi r-2r-\pi r}{2}=r$     AG

[2 marks]